Subject to:
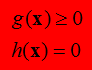
A optimisation problem can be defined as a problem that seeks for a maximum or minimum value for some functions of several variables while, at the same time, satisfying a number of other imposed requirements. The functions are called "Objective" or "Target" functions and the specified requirements are known as the constraints of the problem.
A formulation of a optimisation problem provides a mathematical representation of real-life problems, and the solution process (also called algorithms, programming) generates results that can be used in deciding on the best course of action. This process, from the identification of the problem to the implementation of the solution results in the system, is known as operational research.
The general mathematical (optimisation) programming problem is formulated as:
|
|
|
|
Subject to: |
|
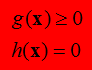f(x) is known as the objective functions. The
set of inequalities and equalities g(x)
0
constitutes the set of the constraints . The objective
function can be subject to maximisation, minimisation or minimax,
and the constraints may have the signs 
,
= and/or . The problem has n unknown decision variables (x) and many
constraints.
A programming (algorithm) attempts to find the set of the values of the unknown variables that satisfy the constraints and optimise the objectives. Mathematical programming techniques are combined in two categories: linear programming and non-linear programming. In Linear programming, both the objective function and constraints must be linear functions. On the other hand, in non-linear programming, one or more of inequalities or equalities are non-linear.
A model will be called as Integer Programming if all the decision variables are integer, or as mixed programming.
Related topics: