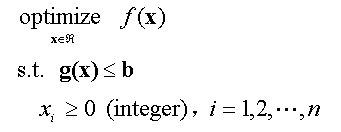
Generally, Reliability Redundancy Allocation Optimization problems can be stated as:
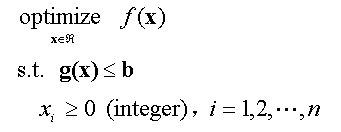
The decision variables are defined as the redundancy number of components. All of them must be integer. The objective function can be the system reliability, availability, or cost. The constraint functions can be the system weight, volume, reliability, availability, or cost of all subsystems. In a given reliability optimization problem, must be maximized or minimized. Therefore we use "optimize" in the statements of the optimization problems. The reliability redundancy allocation optimization, the maintenance personnel allocation optimization and the spares storage allocation optimization belong to this kind of problem.
Definition: In integer reliability redundancy optimization problem. If the point x is belong to the feasible region, and for each k, the new point
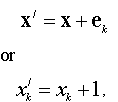
is out of the feasible region , then we say that the point x is a bound point of problem. The collection of such points is the bound region of problem (See Following Figure)
Feasible region of problems |
Solution region of problems |
Bound Theorem: The optimal solution of above problem must be in its bound region (Li, 1996a).
This means that the optimal solution of problem could be obtained by searching in the bound region of the problem. Based on the idea, a few algorithms have been established for solving reliability optimization problems.
Related Publications: